Mass bends space-time! This is a prediction of general relativity, but fortunately we can heuristically derive the effect (up to a factor of 2) using Newtonian mechanics and some simplifying assumptions.
Consider a photon of “mass” mγ passing near an object of mass ML; we’ll call this object a “lens” (the ‘L’ in ML stands for ‘lens’, which is the object doing the bending). The closest approach (b) of the photon is known as the impact parameter. We can imagine that the photon feels a gravitational acceleration from this lens which we imagine is vertical (see diagram).
(a) Give an expression for the gravitational acceleration in the vertical direction in terms of M, b and G.
(b) Consider the time of interaction, ∆t. Assume that most of the influence the photon feels occurs in a horizontal distance 2b. Express ∆t in terms of b and the speed of the photon.
(c) Solve for the change in velocity, ∆v, in the direction perpendicular to the original photon path, over this time of interaction.
(d) Now solve for the deflection angle (α) in terms of G,ML,b, and c using your answers from part (a), (b) and (c). This result is a factor of 2 smaller than the correct, relativistic result.
 |
| Diagram from AY17 WS 4.1 |
(a) Give an expression for the gravitational acceleration in the vertical direction in terms of M, b and G.
We know that gravitational acceleration is the force of Gravity felt by an object divided by that object's mass. We will let gravitational acceleration be represented by \(g\).
\[F_g=\frac{Gym}{r^2}\]
\[g=\frac{GM_L}{r^2}=\boxed{\frac{GM_L}{b^2}}\]
(b) Consider the time of interaction, ∆t. Assume that most of the influence the photon feels occurs in a horizontal distance 2b. Express ∆t in terms of b and the speed of the photon.
All photons travel at the speed of light \(c\), so for this we will use a simple formula:
\[v=\frac{d}{t}\]
\[\boxed{\Delta t =\frac{2b}{c}}\]
(c) Solve for the change in velocity, ∆v, in the direction perpendicular to the original photon path, over this time of interaction.
This draws on simple kinematics.
\[\Delta v=a\times t\]
\[\Delta v= g \Delta t= \boxed{\frac{2GM_L \Delta t}{bc}}\]
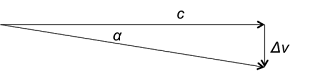
(d) Now solve for the deflection angle (α) in terms of G,ML,b, and c using your answers from part (a), (b) and (c). This result is a factor of 2 smaller than the correct, relativistic result.
Here is where we have to be creative. Nothing can travel faster than the speed of light, so we are going to use an approximation. Note that our new diagram is not in distances but rather in velocities. Using the original velocity vector of the photon c, we will add our new perpendicular vector ∆v.
Conveniently, due to the perpendicular legs, this is a right triangle.
\[tan(\alpha)=\frac{\Delta v}{c}\]
Since the speed of light is ridiculously large, our velocity adjustment is very small in comparison, so our angle is very small. We can thus use a small angle approximation.
\[tan(\alpha) \approx \alpha = \frac{\Delta v}{c}\]
\[\alpha = \frac{2GM_L \Delta t}{bc^2}\]
Adding in the relativistic correction factor gives us:
\[\boxed{\alpha = \frac{4GM_L \Delta t}{bc^2}}\]
nice job.
ReplyDelete5