Stars generate their energy in their cores, where nuclear fusion is taking place. The energy generated is eventually radiated out at the star’s surface. Therefore, there exists a gradient in energy density from the center (high) to the surface (low), but thermodynamic systems tend towards ‘equilibrium.’ In the following sections we will determine how energy flows through the star.
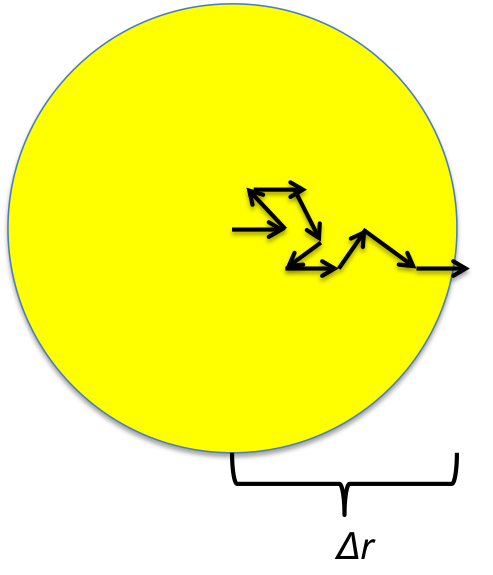
(a) Inside the star, consider a mass shell of width ∆r, at a radius r. This mass shell has an energy density u + ∆u, and the next mass shell out (at radius r + ∆r) will have an energy density u. Both shells behave as blackbodies.
The net outwards flow of energy, L(r), must equal the total excess energy in the inner shell divided by the amount of time needed to cross the shell’s width ∆r. Use this to derive an expression for L(r) in terms of \(\frac{du}{dr}\), the energy density profile. This is the diffusion equation describing the outward flow of energy.
(b) From the diffusion equation, use the fact that the energy density of a blackbody is u(T(r))=aT4 to derive the differential equation:
\(\frac{dT(r)}{dr} \propto -\frac{L(r)\kappa \rho(r)}{\pi r^2 a c T^3}\)
where a is the radiation constant. You just derived the equation for radiative energy transport!
(a) Inside the star, consider a mass shell of width ∆r, at a radius r. This mass shell has an energy density u + ∆u, and the next mass shell out (at radius r + ∆r) will have an energy density u. Both shells behave as blackbodies.
The net outwards flow of energy, L(r), must equal the total excess energy in the inner shell divided by the amount of time needed to cross the shell’s width ∆r. Use this to derive an expression for L(r) in terms of \(\frac{du}{dr}\), the energy density profile. This is the diffusion equation describing the outward flow of energy.
Let's start by finding the energy in a shell. Since a shell is hollow sphere with thickness \(\Delta r\), the energy in the shell is volume times energy density.
\[E=4\pi r^2 \Delta r \Delta u\]
In order to find L(r), we need to divide by the time it takes for a photon to reach the given shell.
\[v_{diff}=\frac{\Delta r}{t}=\frac{lc}{\Delta r}\]
\[t=\frac{\Delta r^2}{lc}\]
\[L(r)=\frac{E}{t}=\frac{4\pi r^2cl\Delta u \Delta r}{\Delta r^2}=4\pi r^2 cl \frac{du}{dr}\]
\[\boxed{L(r)=4\pi r^2 cl \frac{du}{dr}}\]
(b) From the diffusion equation, use the fact that the energy density of a blackbody is u(T(r))=aT4 to derive the differential equation:
\(\frac{dT(r)}{dr} \propto -\frac{L(r)\kappa \rho(r)}{\pi r^2 a c T^3}\)
where a is the radiation constant. You just derived the equation for radiative energy transport!
Let's start by differentiating the energy density equation with respect to T.
\[u(T(r))=aT^4\]
\[du=4aT^3dT(r)\]
The rest is simple. We just substitute \(du\) into our original equation and ignore any coefficients.
\[L(r)=4\pi r^2 cl \frac{du}{dr}\]
\[L(r)=4\pi r^2 cl \frac{4aT^3dT(r)}{dr}\]
\[L(r) \propto \frac{\pi r^2 claT^3dT(r)}{dr}\]
We know that \(l=\frac{1}{\kappa \rho (r)}, suo substituting this gives us:
\[L(r) \propto \frac{\pi r^2 caT^3dT(r)}{\kappa \rho (r) dr}\]
Lastly, we can solve for \(\frac{dT(r)}{dr}\).
\[\boxed{\frac{dt(r)}{dr} \propto -\frac{L(r)\kappa \rho (r)}{\pi r^2 a c T^3}}\]
I worked with G. Grell and S. Morrison to solve this problem.
